R tutorial 3: Changing the root position on a tree branch

When rerooting a phylogenetic tree in APE, instead of midpoint rooting, root is placed closer to one of the child nodes than another. This behavior differs from vizualization in figtree and ggtree::reroot (although ggtree and phytools reroot functions seem to incorrectly handle node-based labels such as support values while rerooting). APE’s root function properly handles such labels, and the way to customize the exact root position on a branch, such that the base of the tree does not appear as a polytomy, is shown below.

Tools needed

We would need the following packages:

• package APE

And the following files:

• phylogenetic tree in newick format

Preparation: simulating and vizualizing the tree

I’m going to show the example with a simulated tree, with simulated node-based support values. Instead, an existing tree may be loaded from the file:

library(ape)

#set seed for replication
set.seed(100)

#simulate the tree
tree <- rtree(20)

#plotting
plot(tree)

#show node labels
nodelabels()

Let’s then reroot this tree, say using t7 as an outgroup. Setting resolve.root to true adds a node along the branch connecting the root taxon and the rest of the tree. Edgelabel set to true would allow root function to account for correct replacement of node labels.

#reroot
tree2 <- root(tree, "t7", resolve.root = T, edgelabel = T)

#plotting
plot(tree2)

#show node labels
nodelabels()

Despite node 21 connects to t7 and node 39, all of 21’s length went to the branch to t7, thus creating an apparent polytomy around the root. This behavior does not appear to depend on whether one of the root’s children is a single tip or not.

One-liner for impatient

Description of the code is in the sections below

#modify root branches
tree2$edge.length[which(!(tree2$edge[,1] %in% tree2$edge[,2]))] <- sum(tree2$edge.length[which(!(tree2$edge[,1] %in% tree2$edge[,2]))])/2

#plotting
plot(tree2)

#show node labels
nodelabels()

Now both branch from 21 to t7 and from 21 to 39 are half as long as the original branch 21 to t7

Explanation of the code

In order to modify the root branch we first need to determine the root node. One visual way to do it is to examine the plot (see fig 2), however it may not be obvious which of the nodes, 21 or 39 is the root one because of the polytomy, and additionally this solution is not scalable. Thus processing of the tree$edge matrix is a better solution. First column of the matrix denotes ancestral nodes, second column their descendands. Root node normally should a non tip node (has some descendants, thus appears in column 1) which at the same time does not have ancestors (thus should not appear in the column 2). Checking for these may yield the root node:

#recreate the rerooted tree for examples below
tree2 <- root(tree, "t7", resolve.root = T, edgelabel = T)

#show the root node
unique(tree2$edge[,1][!(tree2$edge[,1] %in% tree2$edge[,2])])

## [1] 21

Function getRoot() from the package phangorn could be used to determine root node instead, and its solution is a bit more generic. We however interested in branches that descend from the root node, rather than the root node itself, so modifying the command like this:

#show branches connected to the root node
which(!(tree2$edge[,1] %in% tree2$edge[,2]))

## [1]  1 38

will show two branches, first and 38th. Their values are currently:

#show branch length
tree2$edge.length[c(1,38)]

## [1] 0.000000 0.884227

and their location can be confirmed by examining the plot:

#plotting
plot(tree2)

#show node labels
edgelabels()

Here is the relationships between the root node, its branches, how they look in the edge table and on the tree:

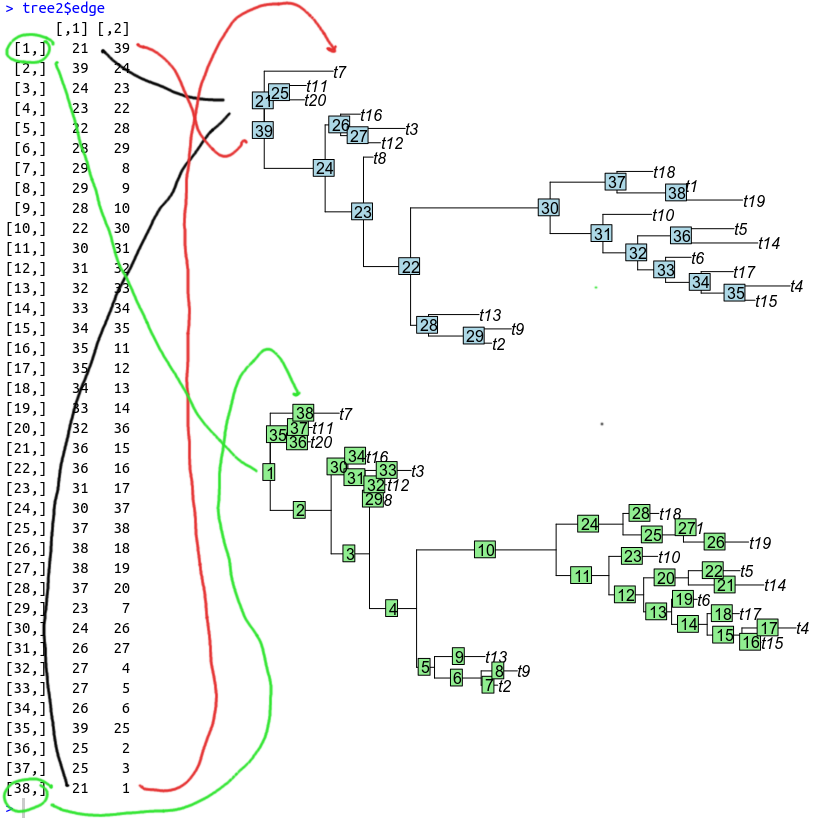
In order to make the root perfectly midpoint, we divide the non-zero length by 2 (or take the sum of the two and divide it). Summation is a more generalized solution, in case second branch is not 0, but the root is still not midpoint. We then assign both branches the obtained values.

tree2$edge.length[c(1,38)] <- sum(tree2$edge.length[c(1,38)])/2

#plotting
plot(tree2)

#show node labels
edgelabels()

Thus putting the code from above into a single command, we get:

tree2$edge.length[which(!(tree2$edge[,1] %in% tree2$edge[,2]))] <- sum(tree2$edge.length[which(!(tree2$edge[,1] %in% tree2$edge[,2]))])/2

In case a non-midpoint position is required, lengths of the two branches can be modified accordingly.